正規表示法(regular expressions)是透過代數來描述語言的一種表達方式, 是在電腦科學被廣為使用的一個概念,此處將會對其作說明
1. 定義
1. 基本定義
- 空集合是正規語言
- 只包含一個空字串的語言是正規語言
- 對任意(字母表集合),是正規語言
- 若A, B是正規語言,則再經過正規語言的運算後依然是正規語言
- 除此之外都非正規語言
2. 符號定義
通常以一個英文字母來代表一個正規表示式,例如a, 而L()就表示一個正規表示式能表達出來的語言(language), 故L(a)代表a這個正規表示式所能表示的語言。
3. 正規語言的運算
正規語言的運算分為
-
聯集(Union) Union (U): 就是把兩個language做聯集. 舉例來說:
-
串接(Concatenation) 把兩個language做連接,這邊的連接不是單純的將兩個正規語言所代表的集合串在一起,而是將元素中的元素作串接。 舉例來說: 語言L跟語言M作串接
則
-
克萊尼星號(Kleene Star) Kleene Star (*): * 表達空集合或是一個L以上的集合聯集的任何子集合。
舉例來說:
2. 引入自動機討論
1. 用$\epsilon-$NFA表示正規表示法
- 基本定義
- 邊線(arc)代表一個symbol,用以連接狀態(state)
-
節點(node)代表automata的狀態
我們可以透過下面將任意的正規表示法轉換成$\epsilon-NFA$

- 延伸
-
聯集(Union): 利用symbol為空字串的arc來造成分支
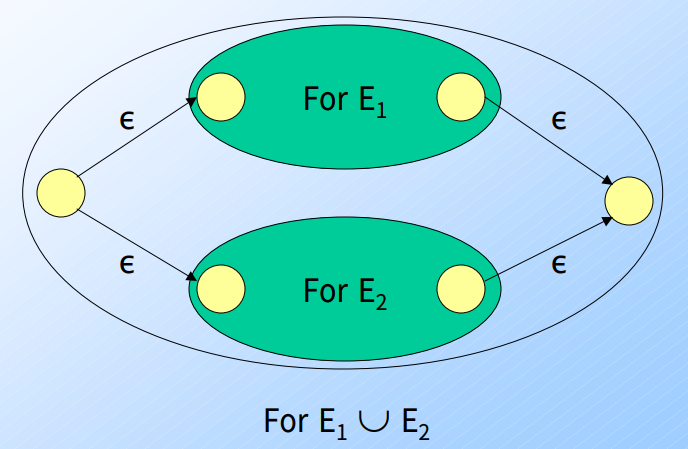
-
串接(Concatenation): 狀態以一symbol為空字串的arc連接
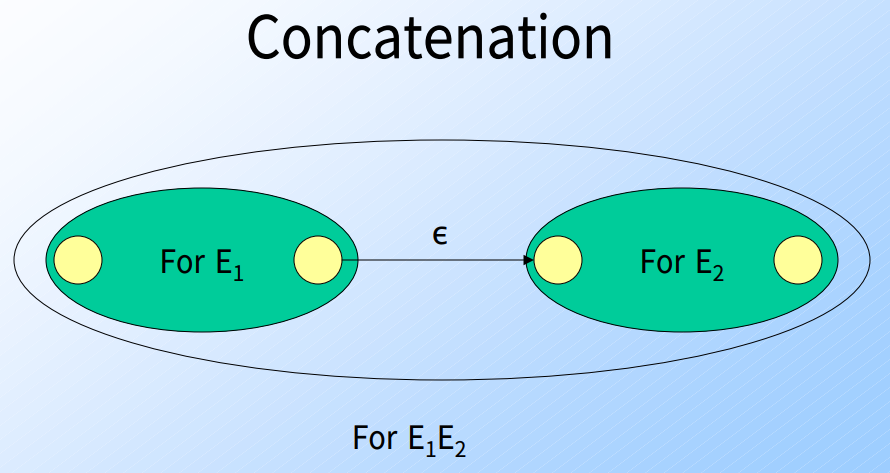
-
克萊尼星號(Kleene Star): 形成迴圈,造成封閉(closure)
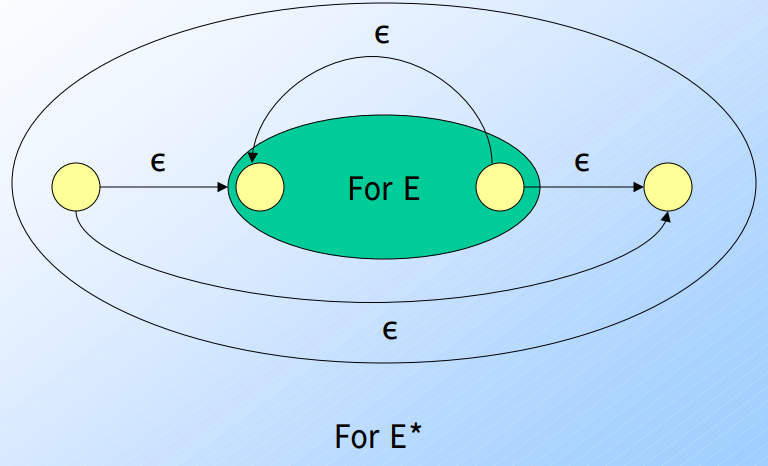
-
2. 用DFA表示正規表示法
- 基本定義:
- 邊線(arc)代表一個symbol\label,用以連接狀態(state)
- 節點(node)代表automata的狀態
- DFA所能接受的路線(path)就是我們的語言(language)
- k-path:
-
定義:
k-path指的是在DFA上不經過狀態編號大於k的路徑,其中終點並不設限,可以是任意的狀態。
-
例子:
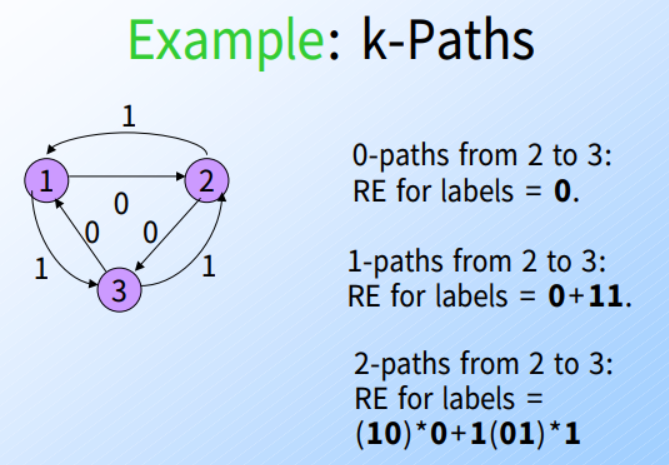
-
- 歸納推導
令$R_{ij}^k$是從狀態$i$到狀態$j$的k-paths的正規表示法,其初始條件如下:
- $k=0$ 時,
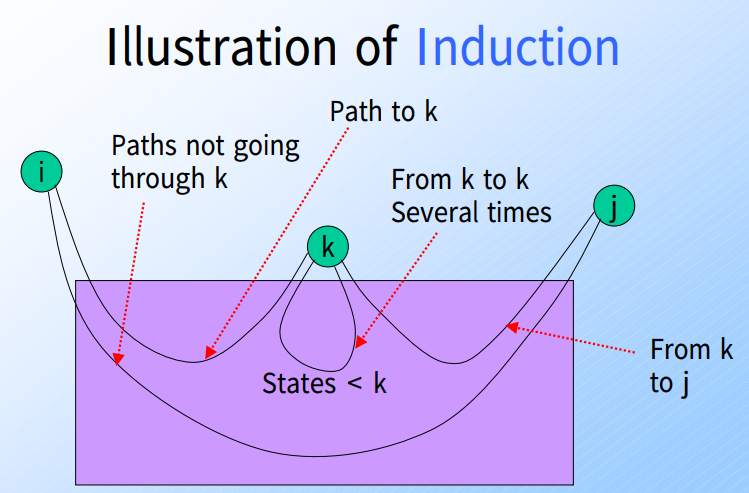
接著可以由此推導出 $R_{ij}^k = R_{ij}^{k-1} + R_{ik}^{k-1}(R_{kk}^{k-1})^*R_{kj}^{k-1}$
$R_{ij}^{k-1}$: 從i到j不經過大於k狀態的path
$R_{ik}^{k-1}$: 從i到k不經過大於k狀態的path
$(R_{kk}^{k-1})^*$: 從k到k不經過大於k狀態的path(零到多次)
$R_{kj}^{k-1}$: 從k到j不經過大於k狀態的path
-
圖解
Stanford Online Course: Automata Theory
自動機理論-Automata筆記-第二週: Regular Expression
圖片來源: